Paper-Rock-Scissors: Balancing in RTS Games

Some of my favorite games are Real-Time Strategy (RTS) games such as StarCraft, Command & Conquer, and Sacrifice. One of the reasons is because RTSs give players the opportunity to "outsmart" their opponents--particular strategies have strengths and weaknesses against others, and if one player can adapt quicker than his opponent, it gives him a definite advantage.

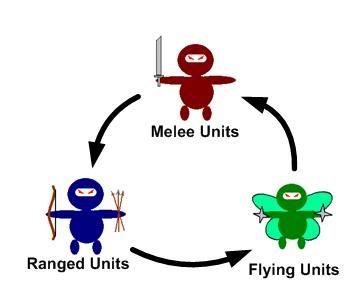
For example, consider the following. Let's say there's a game with three basic types of units: melee, ranged, and flying. The flying units are immune to all melee attacks, but they are weakly armored so they aren't effective against ranged attacks. The ranged units deal additional damage to the flyers, but they also take additional damage from melee attacks. And of course, the melee units have an advantage against ranged but totally ineffective against flying units. In other words, its a basic Paper-Rock-Scissors hierachy.

Let's try to quantify this system in terms of relative effectiveness. For instance, let's say a single melee fighter will have an effectiveness of 1.0 when fighting another melee unit, 2.0 when fighting against a ranged unit, and 0.0 when fighting against a flying unit. That means that one melee unit will be able to defeat a ranged unit in the same amount of time it would take two ranged units and double the time it would take a single ranged unit. No amount of time or additional melee units will be able to overcome a flying unit.

Combat Effectiveness

Unit	vs Melee	vs Ranged	vs Flying
Melee	+1/-1	+2/-1	+0/-1
Ranged	+1/-2	+1/-1	+2/-1
Flying	+1/-0	+1/-2	+2/-2

In this table, the positive number represents the offensive effectiveness and the negative number represents the defensive effectiveness (i.e, how effective the opposing unit's offense is). I chose these particular numbers to try to make each unit's total effectiveness zero-sum. But the question is, are these particular numbers good ones? The goal is to make all units uniformally balanced. Otherwise, certain strategies will be inherently more successful and players will be encouraged to use the strengths of these strategies rather than trying to adapt to his opponents' specific weaknesses.

So the question is, if someone where to create a team of 9 units and play an opponent's unknown team of 9 units, what would his best lineup be? Is there a dominant team that is much more successful than the others? Are there some lineups that are distinctly weak? If so, what could be done to this effectiveness table to make the results more diverse? I've already simulated a lot of possible scenarios, but I'll keep the results saved for my next post.